Generic Orthotopes

Introduction

This page is about generic orthotopes in dimensions 3 and 4. If you haven’t already done so, then you should download and peruse the reference. This page was conceived as a companion to that work.
In particular, we use Scott Vorthmann’s software vZome to visualize 3- and 4-dimensional floral vertices and display an example of a 4-dimensional generic orthotope. We can trace the origin of generic orthotopes to the Zome System, so it is quite natural to use vZome to visualize them.

There are some prerequisites to understanding this page. We expect that a reader understands that a “zone” in a vector space is a partition of the space into mutually parallel lines. For example, it is an important feature of its design that every connected Zometool model uses at most 31 zones (61 if one also uses green struts). In the shapes shown below, we don’t need more than 4 zones. We are fortunate that we may choose 4 yellow zones arranged to have octahedral symmetry. For example, this symmetry is apparent in the all-yellow shadow of the 4-dimensional cube:

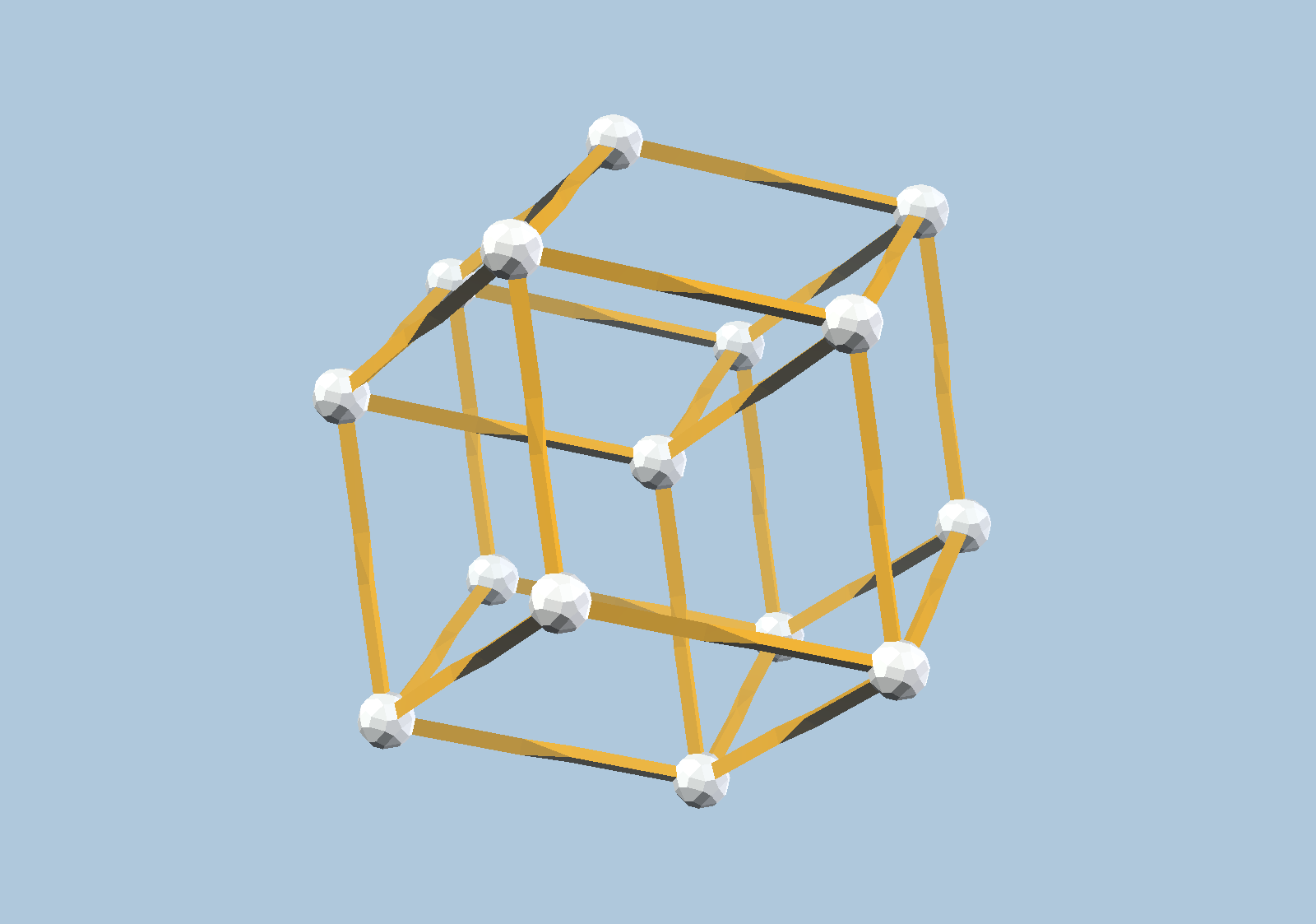
Since generic orthotopes generalize cubes, we expect that the reader is already familiar with this shape. In particular, if you noticed that this graphic shows only one side of the 4-cube and that it has only tetrahedral symmetry, then you are well-positioned to understand the rest of this page.

Nothing but Flowers

Everything about a generic orthotope is floral. The tangent cone at every point of generic orthotope is floral. Every face of a floral vertex is a floral vertex. Every cross section of a floral vertex is a floral arrangement. (It is shown in the reference that a floral arrangement is a cartesian product of a floral vertex with a Euclidean space.) A corollary to these properties of floral tangent cones is that every face and every axis-parallel cross-section of a generic orthotope is a generic orthotope. This will be evident in the example below.

3-Dimensional Floral Vertices

Since every face of a floral vertex is floral, we should acquaint ourselves with 3-dimensional floral vertices before considering 4-dimensional floral vertices. Up to congruence, there are precisely four types of 3-dimensional floral vertices. These appear in the reference, and we may also use vZome to visualize them:

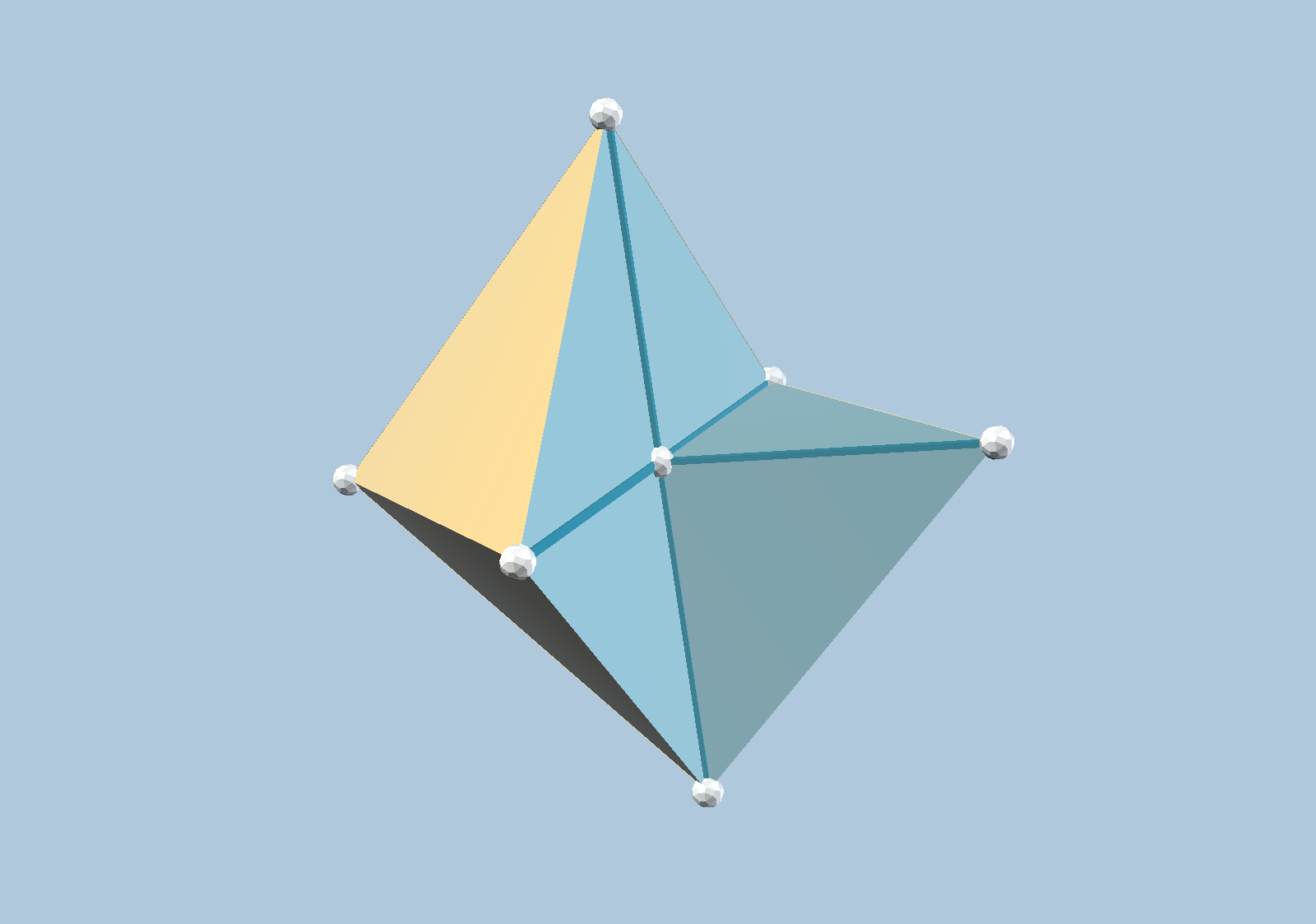
Forming a floral vertex amounts to choosing a particular subset of the orthants in its ambient space. In 3 dimensions, there are precisely 8 orthants, so we call them “octants”. Notice that the vZome graphics illustrate truncations of these four floral vertices, obtained by intersecting each with a regular octahedron centered at the origin and having vertices on the coordinate axes. Thus, the number of octants occupied by each tangent cone coincides with the number of triangles visible in this octahedron.

In the figures above, one should verify that every 2-dimensional face of a 3-dimensional floral vertex is one of the two types of 2-dimensional floral vertices, occupying either 1 or 3 quadrants in the plane. The 1-dimensional faces are merely rays pointing along the coordinate axes.

Axonometric Drawings of Corner Orthotopes

We use dimensional analogy to help understand our visualization of 4-dimensional generic orthotopes. Thus, we first consider 2-dimensional representations of 3-dimensional generic orthotopes and then make observations that will hold analogously in one dimension higher. We restrict our attention to generic orthotopes which are “corner”, meaning that each has an expression as a union of boxes such that the origin is a vertex of all of the boxes and all of the coordinates of the other vertices are non-negative.

Here is a 2-dimensional drawing of a 3-dimensional generic corner orthotope:

We presume the reader is acquainted with this kind of drawing. It is supposed to suggest a solid orthogonal polytope resting snugly against the three coordinate hyperplanes in 3-dimensional space, lying entirely within the primary octant of 3-dimensional Euclidean space (where all coordinates are non-negative). It is also an example of a generic orthotope, as all of its singular points are floral vertices; to verify, notice that every vertex of this solid is congruent to one of the four floral vertices depicted above.

We make some observations in the interests of dimensional analogy. Notice that the drawing above represents a subdivision of the plane into polygonal regions where (a) we use precisely 3 zones in the plane, (b) each polygonal region uses only 2 zones, and (c) there are three rays pointing along the coordinate axes towards the point at infinity. In particular, notice that every 2-dimensional face is a 2-dimensional generic othogon and that there are three “types” of such orthogon, each lacking one of the 3 zones. Picking two coordinate axes, we see that they are part of the boundary of an orthogon. The analogous versions of these hold for 4-dimensional generic corner orthtopes. Thus, in 4 dimensions we should expect a “sculptural” subdivision of 3-dimensional space into 3-dimensional regions which are each a linearly distorted 3-dimensional generic orthotopes. Each of these 3-dimensional faces must use precisely 3 zones and we can distinguish these according to which of the 4 zones these lack. Moreover, we should be able to identify the shadows of the coordinate axes as four lines pointing away towards the point at infinity. And so on.

We also notice that an axonometric drawing of a 3-dimensional floral vertex has an ambiguity, and we presume the reader is acquainted with this ambiguity. For example, a drawing of a single-octant floral vertex could just as well represent a drawing of the 7-octant floral vertex. That is, it is impossible to determine whether the vertex points outward or inward. There is a similar duality between axonometric drawings of the 3-octant and the 5-octant floral vertices. Another way to observe this is that there are only two congruence classes of boundaries of 3-dimensional floral vertices. In the terminlogy in the reference, this is reflected in the conjunctive-disjunctive duality; if v is a conjunctive floral vertex (i.e. a cartesian product of lesser floral vertices), then the complementary arrangement is a disjunctive floral vertex; conversely, if v is disjunctive, then the complement of v is conjunctive.

Boundaries of 4D Floral Vertices

Up to congruence, there are precisely ten types of 4-dimensional floral vertices. These were described in the reference). Because we are “sculpting” these in 3 dimensions, these come in five conjunctive/disjunctive dual pairs. That is, up to equivalence, there are precisely five boundaries of 4-dimensional floral vertices. We show these below:

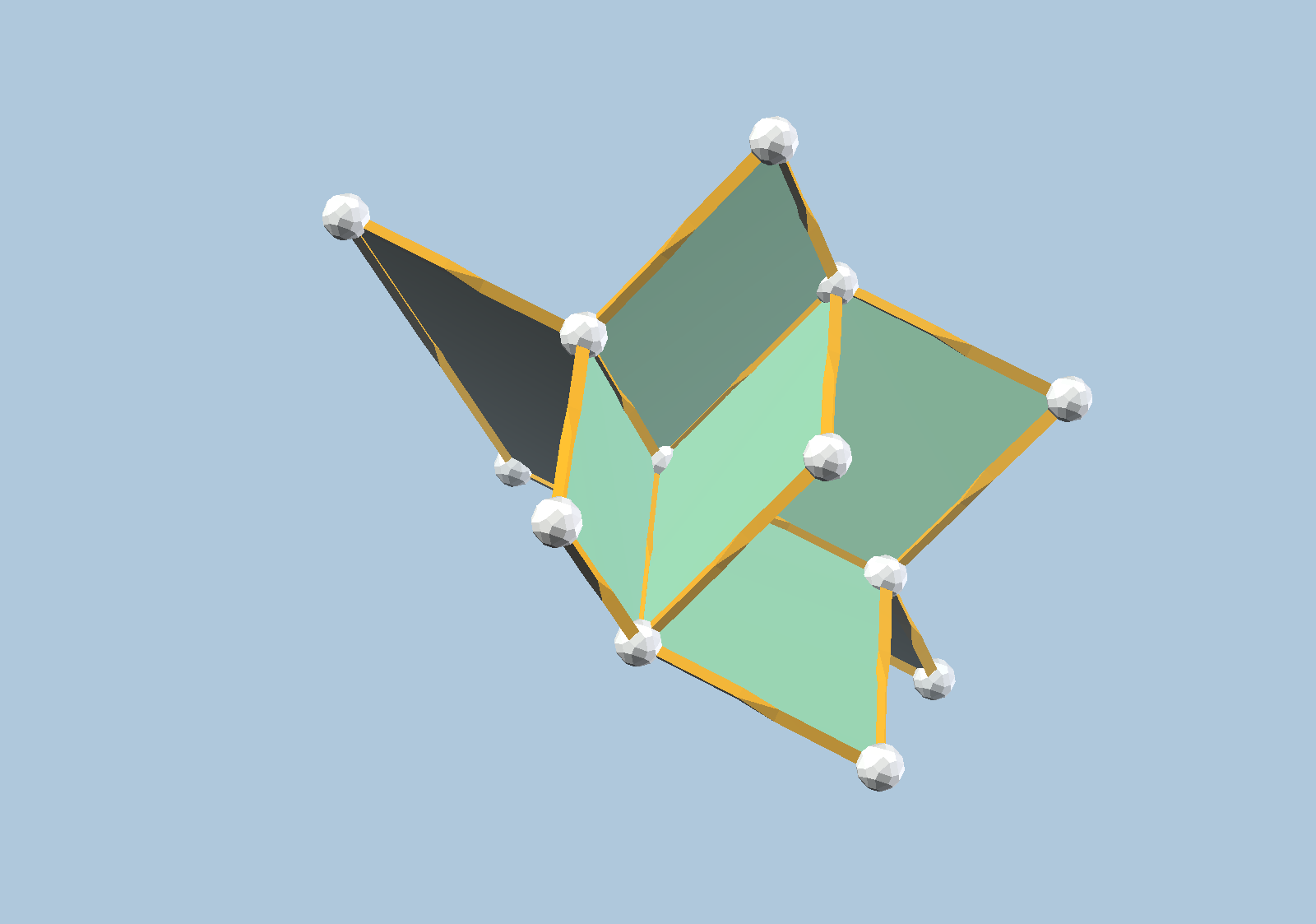
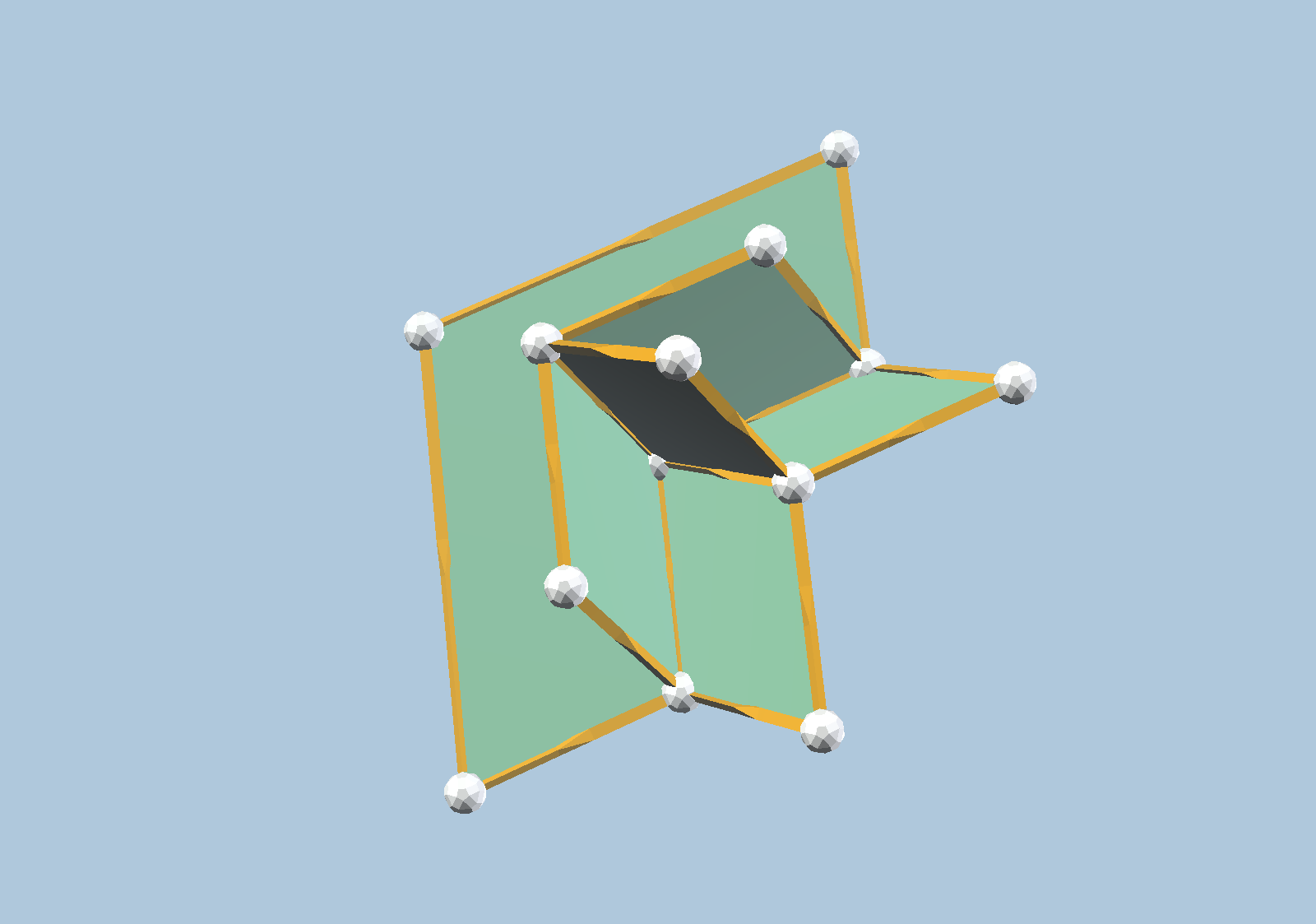
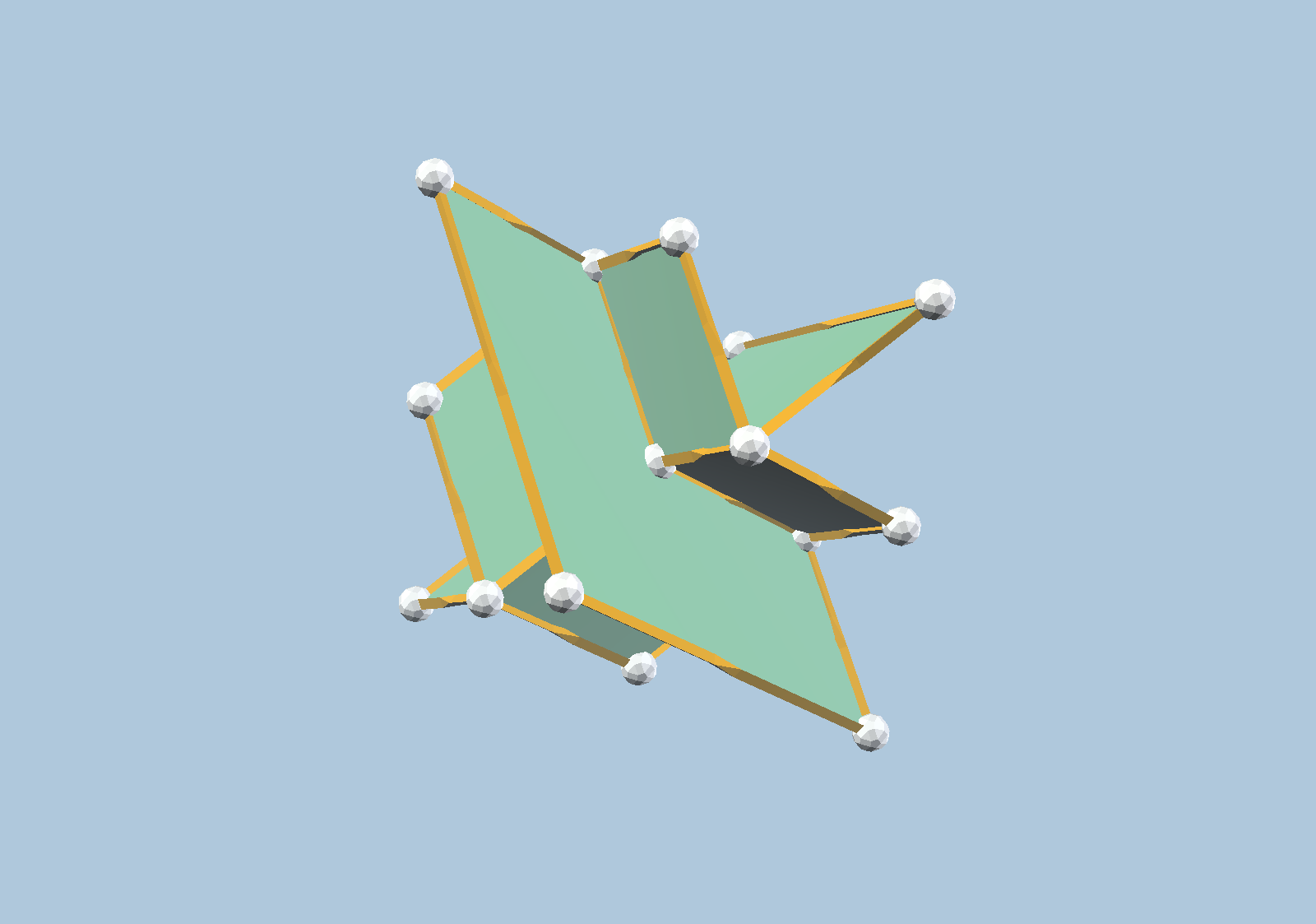
It is a fundamental fact that every floral vertex is simplicial. Thus, we may notice several properties shared among all five figures: (i) There are precisely four edges emanating from each vertex, each using one of 4 prescribed zones. (ii) There are precisely six 2-dimensional panels incident to each vertex, and each of these panels is a linearly distorted 2-dimensional floral vertex (occupying either 1 or 3 quadrants in the plane). (iii) There are precisely four 3-dimensional regions incident to each vertex, subdivided according to the green panels, and each is a linearly distorted 3-dimensional floral vertex. For the last of these, one should compare to the four types of 3-dimensional floral vertices shown earlier.

For example, consider the 4D floral vertex boundary for the pair with 5 or 11 orthants. This has exactly two 3D faces with 1 octant each, one 3D face having 3 octants each, one 3D face having 5 octants, and zero 3D faces having 7 octants. As an exercise, one should make the analogous observation for all five boundaries of 4D floral vertices.

A 4-Dimensional Generic Corner Orthotope

At long last, it is time to see a 4-dimensional generic corner orthotope:

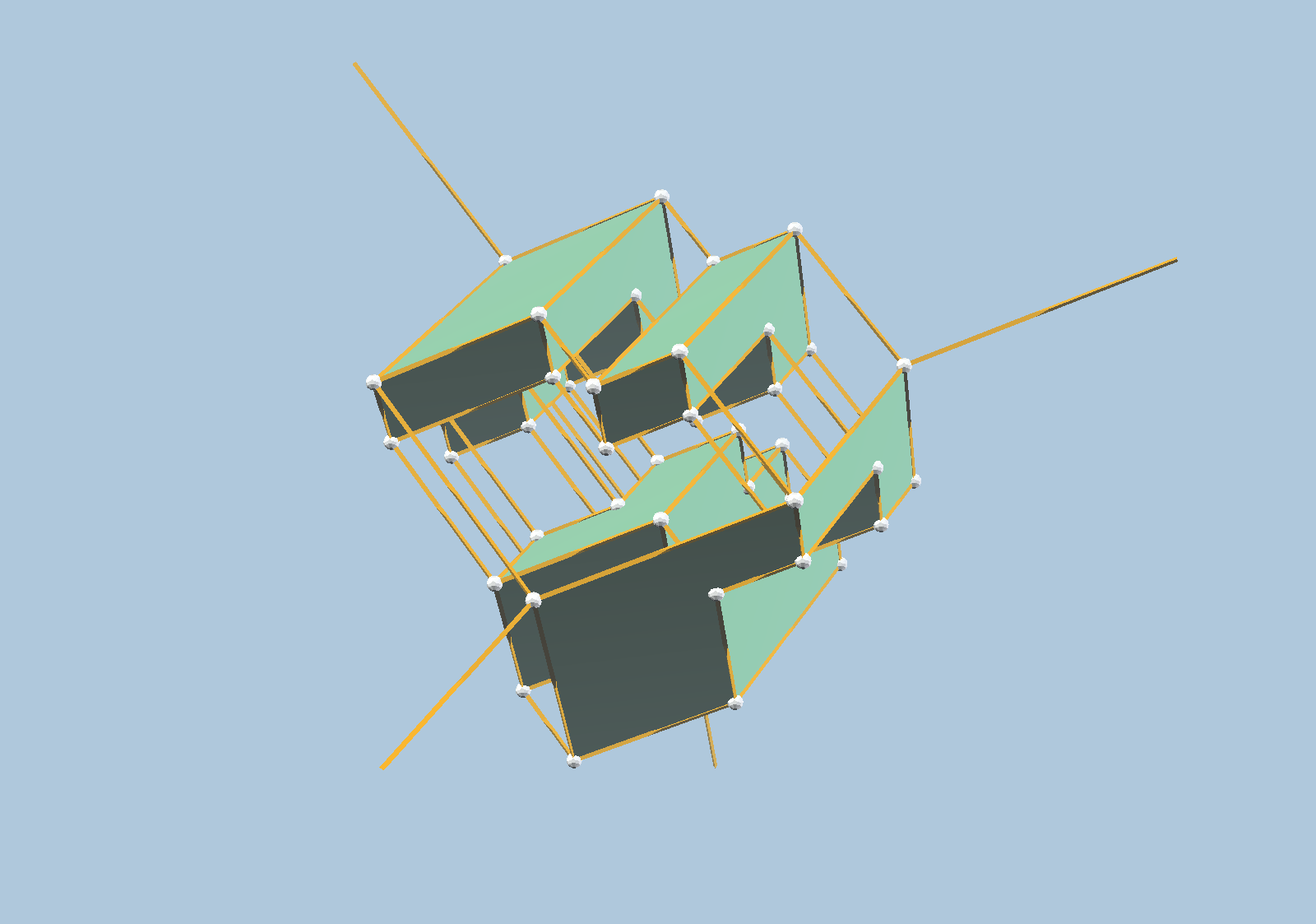
Recall from dimensional analogy that this represents a subdivision of 3-dimensional space in such a way that each of the 3-dimensional regions is a linearly distorted 3-dimensional generic orthotope and every vertex is floral. The reader may inspect to see that every vertex is congruent to one of the floral vertices shown earlier.

In the figure, several mutually parallel faces appear in green. This is intended to emphasize several mutually parallel 3-dimensional faces of this orthogonal polytope. Notice in particular that the solids emphasized by the choices of green planes use only 3 zones.

The model shown in the figure has at least one vertex of each of the ten congruence types of floral vertices. Is this the smallest generic orthotope which has this property? Is this the smallest corner generic orthotope which has this property?

Reference

David Richter. Generic Orthotopes.

---

Home.